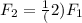Answer: Half as large
Step-by-step explanation:
Newton's law of universal gravitation for Moon 1 is:
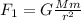 (1)
(1)
And for Moon 2:
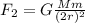 (2)
(2)
Taking into account the mass of Moon 1 is equal to the mass of Moon 2
Where:
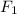 is the gravitational force exerted by the planet on Moon 1
is the gravitational force exerted by the planet on Moon 1
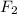 is the gravitational force exerted by the planet on Moon 2
is the gravitational force exerted by the planet on Moon 2
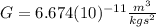 is the Gravitational Constant
is the Gravitational Constant
 is the mass of the planet
is the mass of the planet
 is the mass of each Moon
is the mass of each Moon
 is the distance between the planet and Moon 1
is the distance between the planet and Moon 1
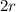 is the distance between the planet and Moon 2
is the distance between the planet and Moon 2
Dividing (2) by (1):
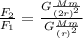

Isolating
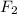 :
: