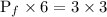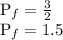Question

g A sample of O2(g) in a 3.0-L container has a pressure of 3.0 atm. If the container volume is changed to 6.0 L, what is the new pressure?

Answer 1

1.5 atm

Step-by-step explanation:

In this question you have make some assumptions to solve this question:

• The container is air tight, it means no exchange of particle is there.
• The temperature of gas inside container is constant, means it is same in both the conditions.
• The gas is considered as ideal gas.

The equation of ideal gas is:

PV=nRT

P: Pressure of gas

V: Volume of gas or container (as volume of gas is same as volume of container when gas is considered as ideal gas)

n: Number of moles of gas in container

R: Universal gas constant = 8.314 J/mole/K = 0.0821 L·atm/mole/K

T: Temperature

In this question n, R and T as considered as constant, only P and V varies.

The initial conditions are:

`\textrm{P}_(i)=3.0\ \textrm{atm}, \ \textrm{V}_(i)=3.0\ \textrm{L}`

`\textrm{P}_(i)\textrm{V}_(i)=\textrm{nRT}`

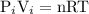
`3*3=\textrm{nRT}` .........eq(1)

The final conditions are:

`\textrm{P}_(f)=? , \ \textrm{V}_(f)=6.0\ \textrm{L}`

`\textrm{P}_(f)\textrm{V}_(f)=\textrm{nRT}`

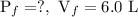
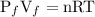
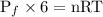`\textrm{P}_(f)*6=\textrm{nRT}` .........eq(2)

Since the right side of eq(1) and eq(2) are equal so the left side will also be equal.

Therefore,
`\textrm{P}_(f)*6=3*3`

`\textrm{P}_(f)=(3)/(2)\\ \textrm{P}_(f)=1.5`