Question

xConsider the following reduction potentials: Cu2+ + 2e– Cu E° = 0.339 V Pb2+ + 2e– Pb E° = –0.130 V For a galvanic cell employing the Cu, Cu2+ and Pb, Pb2+ couples, calculate the maximum amount of work that would accompany the reaction of one mole of lead under standard conditions.

Answer 1

Approximately
`\rm 90\; kJ`.

Step-by-step explanation:

Cathode is where reduction takes place and anode is where oxidation takes place. The potential of a electrochemical reaction (
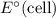`E^(\circ)(\text{cell})`) is equal to

`E^(\circ)(\text{cell}) = E^(\circ)(\text{cathode}) - E^(\circ)(\text{anode})`.

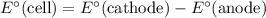There are two half-reactions in this question.
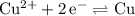`\rm Cu^(2+) + 2\,e^(-) \rightleftharpoons Cu` and
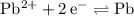`\rm Pb^(2+) + 2\,e^(-) \rightleftharpoons Pb`. Either could be the cathode (while the other acts as the anode.) However, for the reaction to be spontaneous, the value of
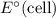`E^(\circ)(\text{cell})` should be positive.

In this case,
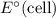`E^(\circ)(\text{cell})` is positive only if
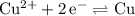`\rm Cu^(2+) + 2\,e^(-) \rightleftharpoons Cu` is the reaction takes place at the cathode. The net reaction would be

`\rm Cu^(2+) + Pb \to Cu + Pb^(2+)`.

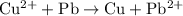Its cell potential would be equal to
`0.339 - (-0.130) = \rm 0.469\; V`.

The maximum amount of electrical energy possible (under standard conditions) is equal to the free energy of this reaction:

`\Delta G^(\circ) = n \cdot F \cdot E^(\circ) (\text{cell})`,

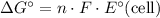where

• 
  `n` is the number moles of electrons transferred for each mole of the reaction. In this case the value of
  `n` is
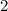  `2` as in the half-reactions.
• 
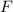  `F` is Faraday's Constant (approximately
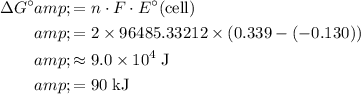  `96485.33212\; \rm C \cdot mol^(-1)`.)

`\begin{aligned}\Delta G^(\circ) &= n \cdot F \cdot E^(\circ) (\text{cell})\cr &= 2* 96485.33212 * (0.339 - (-0.130)) \cr &\approx 9.0 * 10^(4) \; \rm J \cr &= 90\; \rm kJ\end{aligned}`.