Question

A torsion pendulum consists of an irregularly-shaped object of mass 20.0 kg suspended vertically by a wire of torsion constant 0.850 Nm through its center of mass. If this pendulum oscillates through 69 cycles in 66.0 s, find the rotational inertia of the object.

Answer 1

Rotational inertia of the object is,
`I=0.023\ kg-m^2`

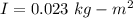
Step-by-step explanation:

Given that,

Mass of the object, m = 20 kg

Torsion constant of the wire, K = 0.85 N-m

Number of cycles, n = 69

Time, t = 66 s

To find,

The rotational inertia of the object.

Solution,

There exists a relationship between the moment of inertia, time period and the torsion constant of the spring is given by :

`T=2\pi\sqrt{(I)/(K)}`

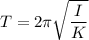
Here I is the moment of inertia

T is the time period, and it is equal to the number of cycles per unit time

`I=(T^2K)/(4\pi ^2)`

`I=((69/66)^2* 0.85)/(4\pi ^2)`

`I=0.023\ kg-m^2`

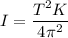
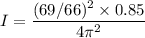
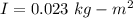
So, the rotational inertia of the object is
`0.023\ kg-m^2`.