Question

A tree falls in a forest. How many years must pass before the 14C activity in 1.03 g of the tree's carbon drops to 1.02 decay per hour? (Carbon-14 has an abundance of 1.3 parts per trillion of carbon-12.)

Answer 1

t = 5.59x10⁴ y

Step-by-step explanation:

To calculate the time for the ¹⁴C drops to 1.02 decays/h, we need to use the next equation:

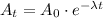`A_(t) = A_(0)\cdot e^(- \lambda t)` (1)

where
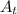`A_(t)`: is the number of decays with time, A₀: is the initial activity, λ: is the decay constant and t: is the time.

To find A₀ we can use the following equation:

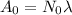`A_(0) = N_(0) \lambda` (2)

where N₀: is the initial number of particles of ¹⁴C in the 1.03g of the trees carbon

From equation (2), the N₀ of the ¹⁴C in the trees carbon can be calculated as follows:

`N_(0) = (m_(T) \cdot N_(A) \cdot abundance)/(m_(^(12)C))`

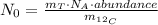
where
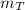`m_(T)`: is the tree's carbon mass,
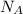`N_(A)`: is the Avogadro's number and
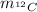`m_(^(12)C)`: is the ¹²C mass.

`N_(0) = (1.03g \cdot 6.022\cdot 10^(23) \cdot 1.3\cdot 10^(-12))/(12) = 6.72 \cdot 10^(10) atoms ^(14)C`

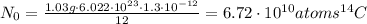
Similarly, from equation (2) λ is:

`\lambda = (Ln(2))/(t_(1/2))`

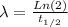
where t 1/2: is the half-life of ¹⁴C= 5700 years

`\lambda = (Ln(2))/(5700y) = 1.22 \cdot 10^(-4) y^(-1)`

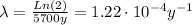
So, the initial activity A₀ is:

`A_(0) = 6.72 \cdot 10^(10) \cdot 1.22 \cdot 10^(-4) = 8.20 \cdot 10^(6) decays/y`

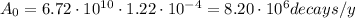
Finally, we can calculate the time from equation (1):

`t = - (Ln(A_(t)/A_(0)))/(\lambda) = - \frac {Ln((1.02decays \cdot 24h \cdot 365d)/(1h\cdot 1d \cdot 1y \cdot 8.20 \cdot 10^(6) decays/y))}{1.22 \cdot 10^(-4) y^(-1)} = 5.59 \cdot 10^(4) y`

I hope it helps you!