Answer:
The estimate of 100- year annual rainfall amount is 274.5cm
Explanation:
From the question, x (mean) =152 ; Sx ( standard deviation) = 30, T (time) 100 years, P (period) = 1/T = 1/100 =0.01
The frequency factor is expressed as:
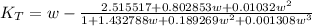
where w=
![[In ((1)/(P^2) )]^(1)/(2)](https://img.qammunity.org/2020/formulas/mathematics/college/h4lkqvy9o3zklwbypxtps1qazn6643zxll.png) for zero is less than P less than or equal to 0.5
for zero is less than P less than or equal to 0.5
w=
![[In ((1)/(0.01^2) )]^(1)/(2)](https://img.qammunity.org/2020/formulas/mathematics/college/nucssf44np4j645ovu1089nvbwgi6xgbfd.png)
= 3.034
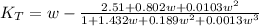

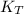 = 2.326
= 2.326

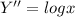
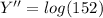
=2.18


=1.477
∴

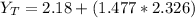
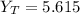
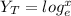
=

=274.5cm