Question

Suppose you deposit into a savings account one cent on January 1, two cents on January 2, four cents on January 03, and so on, doubling the amount of your deposit each day (assume that you use an electronic bank that is open every day of the year). What is the first day that your deposit will exceed $100,000? ANSWER NOW!!

Answer 1

On January 24th the deposit will exceed $100,000

Explanation:

Geometric Progression

Suppose we are forming a sequence where every term can be obtained as the previous term by a constant value called ratio. We can express any term n as

`a_n=a_1r^n`

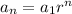
The problem states you deposit into a savings account one cent on January 1, two cents on January 2, four cents on January 3, and so on, each day doubling the previous one

That makes our data like

`a_1=1,\ r=2`

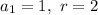
The general term will be

`a_n=2^n`

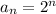
We need to know when your deposit will exceed $100,000, i.e. 10,000,000 cents

In other words, we need to solve for n when

`2^n>10,000,000`

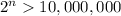
Let's take logarithms in both sides

`ln(2^n)>ln(10,000,000)`

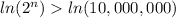
Applying the property of logarithms

`nln(2)>ln(10,000,000)`

Solving for n

`\displaystyle n>(ln(10,000,000))/(ln2)`

`n>23.25`

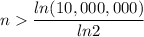
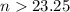
Since n is the number of days since January 1, we use the next integer to ensure the $100,000 are deposited that day

n=24

Answer: On January 24th the deposit will exceed $100,000, exactly $167,772.16