Answer:
On January 24th the deposit will exceed $100,000
Explanation:
Geometric Progression
Suppose we are forming a sequence where every term can be obtained as the previous term by a constant value called ratio. We can express any term n as
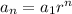
The problem states you deposit into a savings account one cent on January 1, two cents on January 2, four cents on January 3, and so on, each day doubling the previous one
That makes our data like
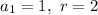
The general term will be
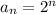
We need to know when your deposit will exceed $100,000, i.e. 10,000,000 cents
In other words, we need to solve for n when
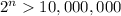
Let's take logarithms in both sides
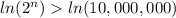
Applying the property of logarithms
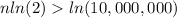
Solving for n
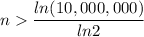
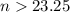
Since n is the number of days since January 1, we use the next integer to ensure the $100,000 are deposited that day
n=24
Answer: On January 24th the deposit will exceed $100,000, exactly $167,772.16