Question

During the time 0.332 mol of an ideal gas undergoes an isothermal compression at 26.4 C, 383 J of work is done on it by the surroundings. The final pressure is 1.87 atm. What was the intial pressure?

Answer 1

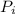`P_(i)` = 2.97 atm

Step-by-step explanation:

The work in thermodynamic processes has several expressions, in the case of isothermal processes the work is

W = n RT ln (
`V_(i)` /
`V_(f)`)

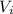Where R is the constant of the ideal gases with a value of 8.314 J / mol K and T the absolute temperature

Let's look for the volume ratio

T = 26.4 +273.15 = 299.55k

Ln (
`V_(i)` /
`V_(f)`)

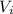= W / n RT

Ln(
`V_(i)` /
`V_(f)`)

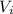= 383 / (0.332 8.314 299.55)

Ln(
`V_(i)` /
`V_(f)`)

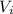= 0.4632

(
`V_(i)` /
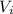`V_(f)`) = e 0.4632

(
`V_(i)` /
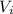`V_(f)`) = 1,589

Let's use the ideal gas equation for two volumes

`P_(i) V_(i)` = n R T

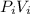`P_(i) V_(i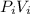)` = n RT

The temperature is the same because it is an isothermal process, this equation is the same

`P_(i) V_(i)` =
`P_(f) V_(f)`

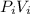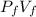
Vi / Vf =
`P_(f)/P_(i)`

`P_(i)`=
`P_(f)`
`V_(i)` /
`V_(f)`

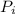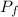
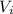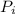`P_(i)` = 1.87 1,589

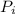`P_(i)` = 2.97 atm