Answer:
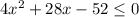
Where, x ≥ 0
Explanation:
Given,
The rectangular picture has,
Length = 6 inches,
Width = 8 inches,
Suppose x be the width( in inch ) of the piece of wooden,
After joining the piece,
New length = 6 + 2x ,
New width = 8 + 2x
So, the area of the final figure,
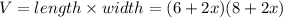
According to the question,
V ≤ 100 inch²
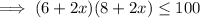
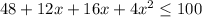
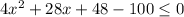
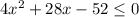
But, width can not be negative,
i.e. x ≥ 0