Question

Solve the proportion using cross products.

Answer 1

Answer: 29 = h

Step-by-step explanation: First, write the problem, 29/58 = 10/h. Next, cross multiply. Write the equation, 58 x 10 = 29h. After, write the equation in a multiplying fraction sentence. 580/29 = 29h/29. Lastly, solve for h by dividing 580 by 29. You should end up with a result of 20 = x.

Answer 2

h = 20

Explanation:

The idea of a "cross product" is that you eliminate denominators by multiplying each numerator by the denominator on the other side of the equality. This is what it looks like:

`\frac{29\,\text{miles}}{58\,\text{hours}}=\frac{10\,\text{miles}}{h\,\text{hours}}\ \longrightarrow\ (29\,\text{miles})(h\,\text{hours})=(10\,\text{miles})(58\,\text{hours})`

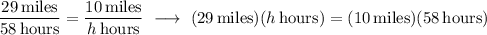
Now, you can divide by the units and the coefficient of h to find ...

`h=(10\cdot 58)/(29)=20`

_____

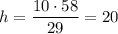
Comment on cross product

IMO, you need to go into the idea of "cross product" with eyes wide open. The rules of equality require that any operation performed on one side of the equation also be performed on the other side. The notion of "cross product" makes it look like you're doing something different to the two sides of the equation.

In fact, the "cross product" is a shortcut for "multiply both sides of the equation by the product of the denominators." Since each denominator term cancels itself, multiplying by the product of denominators looks like multiplying by the other denominator (and throwing away the denominator you have).

__

Another comment on cross product

The idea of "using cross products" is often suggested wherever one fraction is equal to another. In many cases, that is an extra step that is unnecessary.

If the variable is in the numerator, you need only multiply the equation by its denominator, not both of them. If you multiply by both denominators, you find yourself dividing again by the denominator of the fraction not containing the variable. For example, ...

h/10 = 58/29

using cross products, this is ...

29h = 10·58

and we need to divide by the 29 that we just multiplied by.

Instead, we could simply multiply by the denominator of h:

h/10 = 58/29 ⇒ h = 10·58/29