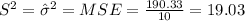Question

An experiment was conducted to observe the effect of an increase in temperature on the potency of an antibiotic. Three 1-ounce portions of the antibiotic were stored for equal lengths of time at each of the following Fahrenheit temperatures: 30?, 50?, 70?, and 90?. The potency readings observed at the end of the experimental period were as shown in the following table. Potency Readings (y) 38, 43, 29 32, 26, 33 19, 27, 23 14, 19, 21. Temperature (x) 30? 50? 70? 90?. a) Find the least-squares line appropriate for this data. b) Plot the points and graph the line as a check on your calculations. c) Calculate S^2

Answer 1

a)
`y=-0.317 x +46.02`

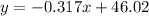
b) Figure attached

c)
`S^2=\hat \sigma^2=MSE=(190.33)/(10)=19.03`

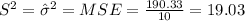
Explanation:

We assume that th data is this one:

x: 30, 30, 30, 50, 50, 50, 70,70, 70,90,90,90

y: 38, 43, 29, 32, 26, 33, 19, 27, 23, 14, 19, 21.

a) Find the least-squares line appropriate for this data.

For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

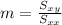
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

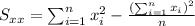
So we can find the sums like this:

`\sum_(i=1)^n x_i = 30+30+30+50+50+50+70+70+70+90+90+90=720`

`\sum_(i=1)^n y_i =38+43+29+32+26+33+19+27+23+14+19+21=324`

`\sum_(i=1)^n x^2_i =30^2+30^2+30^2+50^2+50^2+50^2+70^2+70^2+70^2+90^2+90^2+90^2=49200`

`\sum_(i=1)^n y^2_i =38^2+43^2+29^2+32^2+26^2+33^2+19^2+27^2+23^2+14^2+19^2+21^2=9540`

`\sum_(i=1)^n x_i y_i =30*38+30*43+30*29+50*32+50*26+50*33+70*19+70*27+70*23+90*14+90*19+90*21=17540`

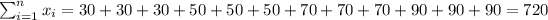
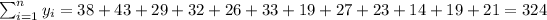
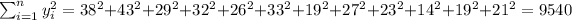
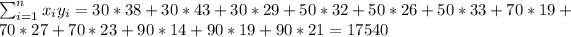
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=49200-(720^2)/(12)=6000`

`S_(xy)=\sum_(i=1)^n x_i y_i -\frac{(\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i)}=17540-(720*324)/(12){12}=-1900`

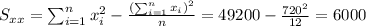
And the slope would be:

`m=-(1900)/(6000)=-0.317`

Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(720)/(12)=60`

`\bar y= (\sum y_i)/(n)=(324)/(12)=27`

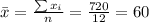
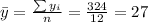
And we can find the intercept using this:

`b=\bar y -m \bar x=27-(-0.317*60)=46.02`

So the line would be given by:

`y=-0.317 x +46.02`

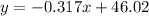
b) Plot the points and graph the line as a check on your calculations.

For this case we can use excel and we got the figure attached as the result.

c) Calculate S^2

In oder to calculate S^2 we need to calculate the MSE, or the mean square error. And is given by this formula:

`MSE=(SSE)/(df_(E))`

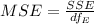
The degred of freedom for the error are given by:

`df_(E)=n-2=12-2=10`

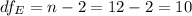
We can calculate:

`S_(y)=\sum_(i=1)^n y^2_i -((\sum_(i=1)^n y_i)^2)/(n)=9540-(324^2)/(12)=792`

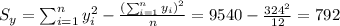
And now we can calculate the sum of squares for the regression given by:

`SSR=(S^2_(xy))/(S_(xx))=((-1900)^2)/(6000)=601.67`

We have that SST= SSR+SSE, and then SSE=SST-SSR= 792-601.67=190.33[/tex]

So then :

`S^2=\hat \sigma^2=MSE=(190.33)/(10)=19.03`