Question

A company is in the business of finding addresses of long lost friends. The company claims to have a 70 % success rate. Suppose that you have the names of seven friends for whom you have no addresses and decide to use the company to track them.

a. Make a histogram sowing the probability of r = 0 to 7 friends for whom an address will be found,
b. Find the mean and the standard deviation of this probability distribution. What is the expected number of friends for whom addresses will be found? (Round your answer to two decimal places),
c. How many names would you have to submit to be 96 % sure that at least two addresses will be found? (Enter your answer as a whole number.)

Answer 1

Following are the solution to this question:

Step-by-step explanation:

In point a:

Consider Binomial ecxperiment for performance probability, p = 0.70.

Therefore, the chance of fail q = 0.30 (1 - 0.70)

N = 9 Sample size

The Binomial likelihood for each success amount could be found using the Excel function BINOMDSIT (x,n,p,0):

`\text{Number of Successes}, x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Probability, P(X=x) \\\\`

`0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=0)=BINOMDIST(0, 9, 0.70, 0) =0.000020\\\\1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=1)=BINOMDIST(1, 9, 0.70, 0) =0.000413\\\\2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=2)=BINOMDIST(2, 9, 0.70, 0) =0.003858\\\\3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=3)=BINOMDIST(3, 9, 0.70, 0) =0.021004\\\\4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=4)=BINOMDIST(4, 9, 0.70, 0) =0.073514\\\\`

`5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=5)=BINOMDIST(5, 9, 0.70, 0) =0.171532\\\\6\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=6)=BINOMDIST(6, 9, 0.70, 0) =0.266828\\\\7\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=7)=BINOMDIST(7, 9, 0.70, 0) =0.266828\\\\8\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=8)=BINOMDIST(8, 9, 0.70, 0) =0.155650\\\\9\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P(X=9)=BINOMDIST(9, 9, 0.70, 0) =0.040354\\\\`

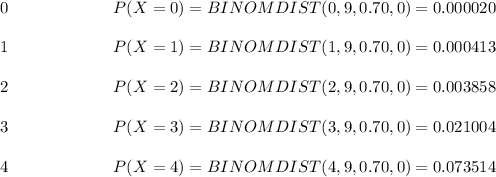
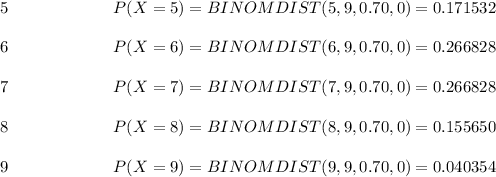
To obtain the necessary Histograms, use X values as just an input X range as well as the probability value values as an output Y range in Excel table in attachment please find it.

In point b:

They recognize that its mean and standard variance of its binomial experiment was,

`Mean = n* p`

`= 9 * 0.70\\\\=6.3\\\\`

`\sigma =√( npq) \\\\`

`= √(9 * 0.70 * 0.30) \\\\ =√(1.89) \\\\ =1.375`

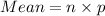
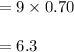
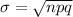
The average is 6.3, so the expected number of friends to whom addresses were found is 6.

In point c:

They must establish the value of n in addition to have
`P(X \geq 2)=0.97`

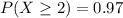
This assertion of probability is replaceable as:

`\to P(X \geq 2) =1-P(X <2 ) =1-P(X \leq 1 )=0.97`

`\to P(X \leq 1 )=(1-0.97)=0.03`

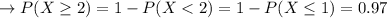
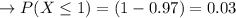
It can be found with the Excel Aim Search feature They must therefore apply approximately 5 identities to be 97% confident that two addresses are found at least.