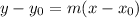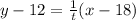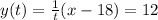Question

Find the equations of the tangents to the given curve that pass through the point (18, 12).

x = 9t2 + 9
y = 6t3 + 6

y = .......... (tangent at smaller t)
y = ..........(tangent at larger t)

Answer 1

`y(t) = (1)/(t)(x - 18}) = 12`

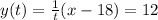
Explanation:

The tangent of a curve is given by the following first degree function:

`y - y_(0) = m(x - x_(0))`

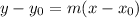
In which
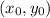`(x_(0), y_(0))` is a function in which the curve pass through and m is the slope, given by the following formula:

`m = ((dy)/(dt))/((dx)/(dt))`

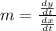
In this problem, we have that:

`x = 9t^(2) + 9`.

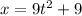So:

`(dx)/(dt) = 18t`

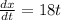
And

`y = 6t^(3) + 6`

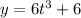
So:

`(dy)/(dt) = 18t^(2)`.

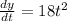Which means that

`m = ((dy)/(dt))/((dx)/(dt)) = (18t)/(18t^(2)) = (1)/(t)`

The curve passes through (18,12). This means that
`x_(0) = 18, y_(0) = 12`.

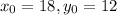So the equation is:

`y - y_(0) = m(x - x_(0))`

`y - 12 = (1)/(t)(x - 18})`

`y(t) = (1)/(t)(x - 18}) = 12`