Question

Someone just robbed a bank. The police set a triangular perimeter of 16 kilometers where the robber may be hiding. Two of the three coordinates for this triangular perimeter are (2, 2) and (-2, -1). Each unit represents a kilometer. The area covered is 12 square kilometers. Which of the following is the third coordinate of the triangular perimeter?

Answer 1

(2,-4)

Explanation:

Test Yourself

Answer 2

The complete question is attached here.

Option A
`(2,-4)` is the third coordinate of the triangular perimeter.

Explanation:

Given

Area=
`12\ km^(2)`

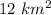
Perimeter=
`16\ km`

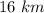
Two of the coordinates ,
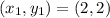`(x_1,y_1)=(2,2)` and
`(x_2,y_2)=(-2,-1)`

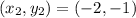
We have to find the third coordinate.

From area of the triangle we can find out the height which can be used to find the stretch of the triangle as the triangle couldn't be stretched beyond its height.

So the height (h)

`(base* height)/(2)=12\ km^(2)`

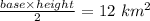
Finding the base using distance formula
`=√((x-x_1)^2+(y-y_1)^2)`

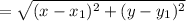
Base
`=√((x_2-x_1)^2+(y_2-y_1)^2) =√((-2-2)^2+(-1-2)^2) =√(16+9) =√(25) =5\ km`

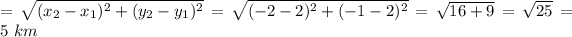
We have assumed this length to be the base of the triangle.

Height
`(12* 2)/(5) =4.8\ km`

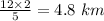
This gives a clue that that in coordinate plane the third points must be less than
`\approx 5\ km`

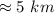
With this option C and D are discarded,we can check it mathematically.

Now we will find the length of the triangle assigning ABC points.

Let
`A=(x_1,y_1)=(2,2)` and
`B=(x_2,y_2)=(-2,-1)`.

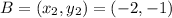Working with the options individually.

Option A
`(2,-4) =C`

`AB=5\ km`

`BC=√((x_3-x_2)^2+(y_3-y_2)^2) =√((-2+2)^2+(-4+1)^2)=√(25) =5\ km`

`AC=√((x_3-x_1)^2+(y_3-y_1)^2) =√((2-2)^2+(-4-2)^2) =√(36)=6\ km`

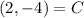
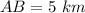
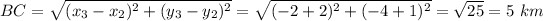
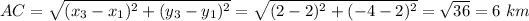
So the perimeter
`AB+BC+AC=(5+5+6)=16\ km`

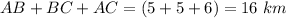
Hence
`(2,-4)` is the third coordinate of the triangle.