Question

For a freely falling object, a(t) = - 32 ft/sec^2, v(0) = initial velocity = v0 (in ft/sec), and s(0) = initial height = S0 (in ft). Find a general expression for s(t) in terms of v0 and s0.

Answer 1

`s(t)=s_(0)+v_(0)t-(0.5)(32)t^(2)`

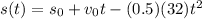
Explanation:

Let's use the definition of acceleration.

`a(t)=dv/dt`

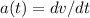
If we take the integral in both sides we will have:

`\int\limits^t_{t_(0)} {a(t)} \, dt=\int\limits^v_{v_(0)} {dv}`

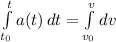
a(t) = -32, so it is independent of time.

`a(t)\int\limits^t_{t_(0)} {dt}=\int\limits^v_{v_(0)} {dv}`

`a(t)(t-t_(0))=v-v_(0)`

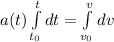
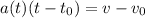
we can assume that
`t_(0) = 0`

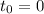
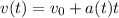`v(t)=v_(0)+a(t)t` (1)

Using the definition of v(t) as the derivative of s (height) with t (time) we have:

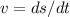`v=ds/dt`(2)

Taking the integral in both sides we can find s(t), and using (1) we have:

`\int\limits^t_{t_(0)} {v(t)} \, dt=\int\limits^s_{s_(0)} {dx}`

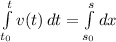
Using (1) in (2)

`\int\limits^t_{t_(0)}( v_(0)+ta(t))\, dt=\int\limits^s_{s_(0)} {ds}`

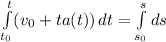
solving this integral, we have:

`v_(0)t+0.5a(t)t^(2)=s(t)-s_(0)`

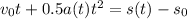
Finally, let's solve this equation for s(t).

`s(t)=s_(0)+v_(0)t+0.5a(t)t^(2)`

`s(t)=s_(0)+v_(0)t-(0.5)(32)t^(2)`

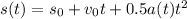
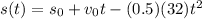
Have a nice day!