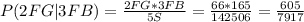Question

In a math class, 12 out of 15 girls are freshmen and 11 out of 15 boys are freshmen. What is the probability that in a randomly selected group of five students from the class, there will be two freshmen girls and three freshmen boys? Express your answer as a common fraction.

Answer 1

`P(2FG|3FB) = (605)/(7917)`

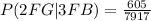
Explanation:

Combinations are a way to calculate the total outcomes of an event where order of the outcomes does not matter.To calculate combinations the below formula is used:

`nCr = (n!)/(r!(n-r)!)`

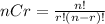
where
`n` represents the total number of items and
`r` represent the number of items being chosen at a time. The '!' represents factorial function which is the product of all integers equal to and less than the given integer. This can be calculated manually using the formula or by using the nCr function on a scientific calculator.

Thus, the number of ways to select 2 freshmen girls (2FG) and 3 freshmen boys (3FB) can be determined. The number of ways to select 5 students (5S) can be determined in the same way.

`2FG = 12C2 = (12!)/(2!(12-2)!) = (12!)/(2!(10)!) = 66`

`3FB = 11C3 = (11!)/(3!(11-3)!) = (11!)/(3!(8)!) = 165`

`5S = 30C5 = (30!)/(5!(30-5)!) = (30!)/(5!(25)!) = 142506`

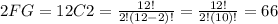
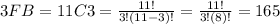
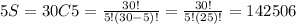
The probability of selecting 2 freshmen girls (2FG) and 3 freshmen boys (3FB) when selecting 5 students out of 30 is given as below:

`P(2FG|3FB) = (2FG*3FB)/(5S) = (66*165)/(142506) = (605)/(7917)`