Question

A 16 lb block rests on a horizontal frictionless surface. A cord attached to the block, running horizontally, passes over a pulley whose diameter is 10 in, to a hanging block weighing 16 lb. The system is released from rest, and the blocks are observed to move 7 ft in 2 s. What is the moment of inertia of the pulley (in slug-feet^2)?

Answer 1

I = 6.2161900319309 slug-feet^2[/tex]

Step-by-step explanation:

The moment of inertia of an object may simply be stated as a measure of how difficult it is to start it spinning, or to alter an object's spinning motion

The moment of inertia of an object is given by the expression

`I=mr^(2)`

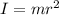
but in this case we are talking about the moment of inertia of a circular disk, the expression is a bit different

`I=[tex](1)/(2)`mr^{2}[/tex]

inputting the values given in the expression above

`I=(1)/(2)(16)5^(2)`

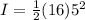
moment of inertia = 200 lb

the expected outcome should be in slug feet squared

1 slug-feet squared = 32.1740488782426

therefore we need to divide our answer by this value

so

=
`(200)/(32.1740488782426) \\</p><p>= 6.2161900319309  slug-feet^2`