Answer:
The y coordinate is -7.999 ≈ -8
Explanation:
One of the points on line segment is given as (-2,2).
The distance given is 10.049 units.
The x coordinate of other point is given as -3. Thus the point is (-3 , y),
where y is y coordinate of point lying in third quadrant.
The distance formula is given as,
Distance =
 , where
, where
(x1,y1) and (x2,y2) are endpoints of line segment.
Inserting above two points and equating to 10.049 units,
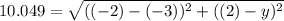
Squaring both the sides,

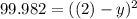
+9.999 = (2-y) or -9.999 = (2-y)
y = 2-9.999 or y = 2+9.999
y = - 7.999 0r 11.999
But, point lies in third quadrant and is negative.
thus, y = -7.999