The amount in account for 7 years is $ 10594.96
Solution:
Given that peter deposited $6500 into an account paying annual interest 7% compound monthly
To find: Total amount in account after 7 years
The formula for total amount using compound interest is given as:
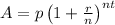
Where "p" is the principal amount
"A" is the future value of the investment/loan, including interest
"r" is annual interest rate (decimal)
"n" is the number of times interest is compounded per unit "t"
"t" is the time the money is invested
Here in this sum,
p = $ 6500
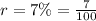
t = 7 years
n = 12 (since interest is compounded monthly, and there are 12 months in one year)
Substituting the values in formula, we get

Thus the amount in account for 7 years is $ 10594.96