Question

From an urn with 6 red balls and 4 blue balls, two balls are picked randomlywithout replacement. Find the probability that both balls picked are red.

Answer 1

The probability that both balls picked are red is 0.3333

Explanation:

Total number of balls = 6 + 4 = 10

Total number of red balls = 6

Total number of blue balls = 4

Probability is the ratio of number of favorable outcome to total number of outcomes.

`\texttt{Probability of drawing first red ball = }\frac{\texttt{Number of red balls}}{\texttt{Total number of balls}}\\\\\texttt{Probability of drawing first red ball = }(6)/(10)\\\\\texttt{Probability of drawing second red ball = }\frac{\texttt{Number of red balls}}{\texttt{Total number of balls}}\\\\\texttt{Probability of drawing second red ball = }(5)/(9)`

`\texttt{Probability of drawing two red balls = }\texttt{Probability of drawing first red ball}* \texttt{Probability of drawing second red ball}\\\\\texttt{Probability of drawing two red balls = }(6)/(10)* (5)/(9)=0.333`

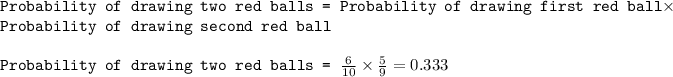
The probability that both balls picked are red is 0.3333