Question

Let f be a continuous function defined on the interval [0,1] such that f(0) = f(1). Show that there exists a number 0 <= a <= 1/2 such that f(a) = f(a+1/2)

Answer 1

Step-by-step explanation:

In order to prove that affirmation, we define the function g over the interval [0, 1/2] with the formula
`g(x) = f(x+1/2)-f(x) .`

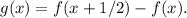
If we evaluate g at the endpoints we have

g(0) = f(1/2)-f(0) = f(1/2) - f(1) (because f(0) = f(1))

g(1/2) = f(1) - f(1/2) = -g(0)

Since g(1/2) = -g(0), we have one chance out of three

• g(0) > 0 and g(1/2) < 0
• g(0) < 0 and g(1/2) > 0
• g(0) = g(1/2) = 0

We will prove that g has a zero on [0,1/2]. If g(0) = 0, then it is trivial. If g(0) ≠ 0, then we are in one of the first two cases, and therefore g(0) * g(1/2) < 0. Since f is continuous, so is g. Bolzano's Theorem assures that there exists c in (0,1/2) such that g(c) = 0. This proves that g has at least one zero on [0,1/2].

Let c be a 0 of g, then we have

`0 = g(c) = f(c+1/2)-f(c)`

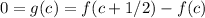
Hence, f(c+1/2) = f(c) as we wanted.