Question

The percent of remaining parent isotope in a radioactive decay process is 40 percent. How many half-lives have elapsed since the material was 100 percent parent atoms?

Answer 1

Answer: Between 1 and 2.

Step-by-step explanation:

Half life is the amount of time taken by a radioactive material to decay to half of its original value.

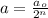`a=(a_o)/(2^n)` ............(1)

where,

a = amount of reactant left after n-half lives = 40

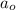`a_o` = Initial amount of the reactant = 100

n = number of half lives

Putting in the values we get:

`40=(100)/(2^n)`

`2^n=2.5`

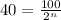
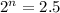
taking log on both sides

`nlog(2)=log(2.5)`

`n=1.32`

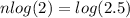
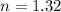
Thus half-lives that have elapsed is between 1 and 2