Question

What is the range of the function y = -3cosx + 1?

-4 ≤ x ≤ 4
-3 ≤ x ≤ 3
-3 ≤ x ≤ 4
-2 ≤ x ≤ 4

Answer 1

`-2\leq x\leq 4`

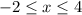
Explanation:

Recall that the function cos(x) shows an oscillating curve between the values -1 and 1 on the vertical axis (the Range of this goes therefore between y = -1 to y=1).

Now, when you multiply this trig function by "-3", its amplitude increases, and therefore it will be now oscillating between the values y=-3 and y=3.

if to this, you now add 1 (to complete the function: f(x) = -3 cos(x) +1, you are translating the full function one unit up. Then the new function will be still oscillating, but between the values y=-2 and y = 4 (the previous ones shifted up by 1 unit)

Therefore, the answer to the question is:

Range of f(x) is {
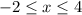`-2\leq x\leq 4`}, which coincides with your last answer choice.