Question

Type the correct answer in each box. Use numerals instead of words. Consider this quadratic equation. x2 + 2x + 7 = 21 The number of positive solutions to this equation is . The approximate value of the greatest solution to the equation, rounded to the nearest hundredth, is .

Answer 1

This quadratic equation has only 1 positive solution, and the greatest solution is 2.87, rounded to the nearest hundredth.

Explanation:

The given expression is

x^{2}+2x+7=21

To solve this expression, we need to pass all terms to the left side

`x^(2)+2x+7=21\\x^(2)+2x+7-21=0\\x^(2)+2x-14=0`

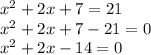
Now, we solve the equation using the quadratic formula

`x_(1,2)=\frac{-b\±\sqrt{b^(2)-4ac} }{2a}`

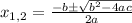
Where

`a=1\\b=2\\c=-14`

Replacing these values, we have

`x_(1,2)=\frac{-2\±\sqrt{2^(2)-4(1)(-14)} }{2(1)}\\x_(1,2)=(-2\±√(4+56) )/(2)=(-2\±√(60) )/(2)  \\x_(1)\approx 2.9\\x_(2)\approx -4.9`

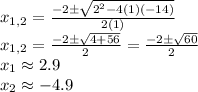
Therefore, this quadratic equation has only 1 positive solution, and the greatest solution is 2.87, rounded to the nearest hundredth.