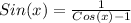Answer:
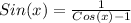
Explanation:
Here, given :
sin 2 x - 2 sin x = 2 .... (1)
Now, by TRIGONOMETRIC IDENTITY:
Sin 2Ф = 2 SinФ CosФ
⇒ sin 2 x = 2 sin x cos x
Putting back the value in (1), we get:
sin 2 x - 2 sin x = 2 ⇒ (2 sin x cos x) - 2 sin x = 2
or, 2( sin x cos x - sin x) = 2
or, sin x cos x - sin x = 1
or, (sin x) ( cosx - 1) = 1
⇒ Sin x = 1 / ( Cos x - 1)
Hence,