Question

A rectangular prism (box) has a length of 21 m, a width of 12 m, and a height of 16 m. Find the length of the greatest possible straight-line segment that can be contained in this box.

Answer 1

29 meters

Explanation:

Given: A rectangular prism (box) has a length of 21 m, a width of 12 m, and a height of 16 m.

To find: The length of the greatest possible straight-line segment that can be contained in this box.

Solution: In a rectangular prism(box), the largest length of the greatest possible line segment is the diagonal of the prism.

Now, we know that if l, b, and h are the length, width and height of the prism.

The diagonal of the prism is
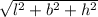`\sqrt{l^(2)+b^(2) +h^(2)}` units.

Here, length is 21 m, width is 12 m and a height of 16 m.

So, length of the diagonal is

`\sqrt{21^(2)+12^(2)+16^(2) } \\`

`=√(441+144+256)`

`=√(841)`

`=29`

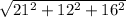
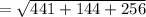
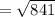
Hence, the length of the largest line-segment that can be contained in the box is 29 meters.