The required explicit formula is
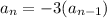
Solution:
Given that sequence is -4, 12, -36, 108
To find: explicit formula
Explicit formulas define each term in a sequence directly, allowing one to calculate any term in the sequence
An explicit formula designates the nth term of the sequence, as an expression of n (where n = the term's location). It defines the sequence as a formula in terms of n.
Let us first find the logic used in sequence
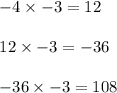
So we can see clearly that next term in sequence is obtained by multiplying -3 with previous term
This can be defined in terms of "n"
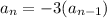
Where
 represents the next terms location and
represents the next terms location and
 represents previous term location
represents previous term location
So the required explicit formula is
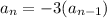
Let us verify our explicit formula
Now let us find the 4th term of sequence
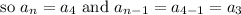
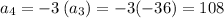
Thus using the explicit formula, next terms in sequence can be found