Question

An architect is sketching a blueprint of a patio for a new fence. On the blueprint, C is the midpoint of segment AD. Point B is the midpoint of segment AC. If BC = 8 feet, what is the length of AD?

Answer 1

The length of AD is 32 feet

Explanation:

Proportional distances

When distances are proportions of others, we can express all of them as relative fractions until we reach some known distance and solve for the desired length

Let's call x the length of AD. Given C is the midpoint of AD, then

`\displaystyle AC=CD=(x)/(2)`

Given B is the midpoint of AC, then

`\displaystyle AB=BC=(AC)/(2)=(x)/(4)`

If we know BC=8 feet

`\displaystyle (x)/(4)=8\ feet`

`\displaystyle x=32\ feet`

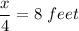
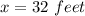
The length of AD is 32 feet