Question

Which statements are true about the ordered pair (5

- 6) and the system of equations?
x + y = -1
| 3x - y = 21
Select each correct answer.
- 6) is a solution to the first equation because it makes the
The ordered pair (5
first equation true.
The ordered pair (5 - 6) is a solution to the second equation because it makes
the second equation true.
The ordered pair (5 - 6) is not a solution to the system because it makes at least
one of the equations false.
The ordered pair (5,
equations true.
- 6) is a solution to the system because it makes both

Answer 1

The ordered pair (5,-6) is a solution to the first equation because it makes the first equation true

The ordered pair (5 - 6) is a solution to the second equation because it makes the second equation true

The ordered pair (5 - 6) is a solution to the system because it makes both equations true

Explanation:

we have

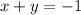`x+y=-1` --- equation A

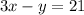`3x-y=21` ----> equation B

we know that

If a ordered pair is a solution of the system of equations, then the ordered pair must satisfy both equations

Solve the system of equations by elimination

Adds equation A and equation B

`x+y=-1\\3x-y=21\\-----\\x+3x=-1+21\\4x=20\\x=5`

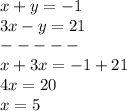
Find the value of y

substitute the value of x in any equation

`x+y=-1`

`5+y=-1`

`y=-6`

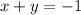
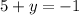
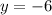
The solution of the system is the point (5,-6)

therefore

Verify each statement

a) The ordered pair (5,-6) is a solution to the first equation because it makes the first equation true.

The statement is true (see the procedure)

b) The ordered pair (5 - 6) is a solution to the second equation because it makes the second equation true

The statement is true (see the procedure)

c) The ordered pair (5 - 6) is not a solution to the system because it makes at least one of the equations false

The statement is false (see the procedure)

d) The ordered pair (5 - 6) is a solution to the system because it makes both equations true

The statement is true (see the procedure)