The expression for length of rectangle is (x - 16) units
Solution:
Given that area of a rectangle is represented by
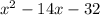 square units
square units
width of the rectangle is represented by (x+2) units
To find: length of the rectangle
The area of rectangle is given as:
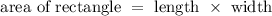
Substituting the values in formula, we get
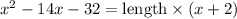 ---- eqn 1
---- eqn 1
Let us first factorise the L.H.S of eqn 1
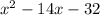
Break the expression into groups
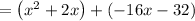
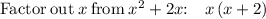

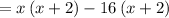
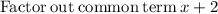
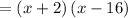
Now substitute the above value in eqn 1
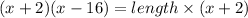
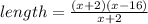
Length = x - 16
Thus the expression for length of rectangle is (x - 16) units