Answer:
reject H0
Explanation:
Given that a researcher is testing the claim that adults consume an average of at least 1.85 cups of coffee per day.
A sample of 35 adults shows a sample mean of 1.70 cups per day with a sample standard deviation of 0.4 cups per day.
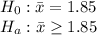
(right tailed test at 5% level of significance)
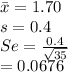
Test statistic t = mean difference/std error =
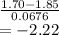
df = 34
t critical = -1.697
Since our test statistic < t critical we reject null hypothesis..