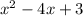Question

Identify a quadratic function that fits the points (−1, 8),(2, −1), and (0, 3).

Answer 1

The quadratic equation is y =
`x^(2) - 4x +3`

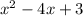
Explanation:

Let the quadratic equation be y = f(x) =
`ax^(2) +bx+c`

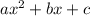
The graph of this quadratic equation should pass through all the given points.

The given points are (-1,8),(2,-1) and (0,3).

y =
`ax^(2) +bx+c`

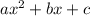
We have to substitute the 3 points in the general equation and solve to find the values of a,b and c.

Substitute (-1,8) ,

8 =
`a(-1)^(2) + b(-1) + c`

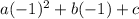
8=a - b + c -------------------------(1)

Substitute (2,-1) ,

-1 =
`a(2)^(2) + b(2) +c`

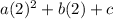
-1 = 4a + 2b + c --------------------------(2)

Substitute (0,3) ,

3 =
`a(0)^(2) + b(0) +c`

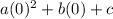
3 = c

c = 3 --------------------------(3)

Substitute (3) in (1) and (2) ,

8 = a - b + c

8 = a - b + 3

a - b = 5

a = b + 5 --------------------------(4)

4a + 2b + c = -1

4a + 2b + 3 = -1

4a + 2b = -4

2a + b = -2 --------------------------(5)

Substitute (4) in (5) ,

2a + b = -2

2\times (b + 5) + b = -2

2b +10 +b = -2

b = -4

Substituting value of b in (4) ,

a = 1

Hence the quadratic equation is y =
`x^(2) - 4x +3`