Question

A meter stick is suspended vertically at a pivot point 22 cm from the top end. It is rotated on the pivot until it is horizontal and then released from rest. What will be its maximum angular velocity (in radians/second)?

Answer 1

5.82812 rad/s

Step-by-step explanation:

L = Length of meter stick = 1 m = 100 cm

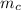`m_c` = The center of mass of the stick =
`(L)/(2)-0.22=0.5-0.22=0.28\ m`

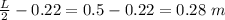
`\omega` = Angular velocity

Moment of inertia of the system is given by

`I=I_c+mr^2\\\Rightarrow I=(mL^2)/(12)+mr^2\\\Rightarrow I=(m1^2)/(12)+m0.28^2\\\Rightarrow I=m((1)/(12)+0.0784)`

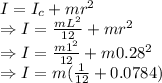
As the energy in the system is conserved

`mgh=I(\omega^2)/(2)\\\Rightarrow mgh=m((1)/(12)+0.0784)(\omega^2)/(2)\\\Rightarrow gh=((1)/(12)+0.0784)(\omega^2)/(2)\\\Rightarrow \omega=\sqrt{(2gh)/((1)/(12)+0.0784)}\\\Rightarrow \omega=\sqrt{(2* 9.81* 0.28)/((1)/(12)+0.0784)}\\\Rightarrow \omega=5.82812\ rad/s`

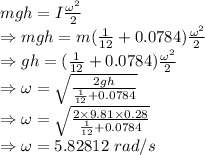
The maximum angular velocity is 5.82812 rad/s