Answer:
The angular velocity is 35.5 rad/s.
Step-by-step explanation:
Step 1: Find the moment of Inertia for the rod
The moment of inertia, I, of a rod:
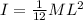 .......... (1)
.......... (1)
where M = mass of rod (0.78 Kg); L = Length of rod (0.54 m).
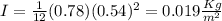
Step 2: Calculate the angular acceleration from Rotational kinetic notation
F.r = I.α ........... (2)
where F is the force acting upon the rod; r is the half length of the rod; I is the moment of Inertia and; α is the angular acceleration.
∴ (1000 N)(0.27 m) = 0.019α
α = 270 Nm / 0.019 Kgm²
α = 14210.5 rad/s
Step 3: We find the angular velocity by using the equation below:
ωf = ωi + αt ......... (3)
where
ωf is the angular velocity after the blow
ωi is the angular velocity before the blow = 0
t is the time taken for the blow to occur = 2.5 ms
ωf = 0 + (14210.5 rad/s)(2.5 ms) = 35.5 rad/s.