Option C
The common ratio for this geometric sequence 0.7, 1.4, 2.8, 5.6, ... is 2
Solution:
Given geometric sequence is:
0.7, 1.4, 2.8, 5.6, ...
To find: common ratio for this geometric sequence
A geometric sequence is a sequence of numbers that follows a pattern were the next term is found by multiplying by a constant called the common ratio, "r"
In the given sequence, the next term in squence is found out by multiplying previous term by 2
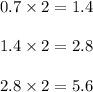
So the common ratio in given sequence is 2
Method 2:
Given geometric sequence is:
0.7, 1.4, 2.8, 5.6, ...
Here first term
 and
and

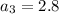 and
and

Common ratio can be found by:
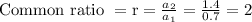

Thus the common ratio is 2