Question

The graph shows the function f(x)=−6x−12 and g(x)=(12)x−4 . What are the solutions of the equation −6x−12=(12)x−4 ? x = 12 and x = 0 ​ x=−4 ​ and x = 12 ​ x=−12 ​ and ​x = 12​ ​ x=−4 ​ and x=−2 A line and an exponential curve is graphed on a coordinate plane. The horizontal x-axis ranges from negative 10 to 10 in increments of 1. The vertical y-axis ranges from negative 10 to 10 in increments of 1. The curve is labeled g open argument x close argument and approaches, never touches or crosses below y equals negative 4 in the fourth quadrant. The curve decreases through begin ordered pair negative 2 comma 0 end ordered pair. The curve passes through begin ordered pair negative 4 comma 12 end ordered pair and begin ordered pair 0 comma negative 3 end ordered pair and exits the fourth quadrant. A line is labeled f open argument x close argument and passes through begin ordered pair negative 4 comma 12 end ordered pair and begin ordered pair 0 comma negative 12 end ordered pair. The line intersects the curve at begin ordered pair negative 4 comma 12 end ordered pair and begin ordered pair negative 2 comma 0 end ordered pair.

Answer 1

The solutions are x=-4 and x=-2

Explanation:

we have

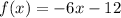`f(x)=-6x-12` ----> equation A

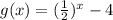`g(x)=((1)/(2))^(x)-4` ----> equation B

The solutions of the equation
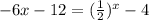`-6x-12=((1)/(2))^(x)-4` are the x-coordinates of the intersection points both graphs

using a graphing tool

The intersection points both graphs are (-4,12) and (-2,0)

see the attached figure

therefore

The solutions are x=-4 and x=-2