Question

A uniform stick 1.0 m long with a total mass of 270 g is pivoted at its center. A 3.0 g bullet is shot through the stick midway between the pivot and one end. The bullet approaches at 250 m/s and leaves at 140 m/s. With what angular speed is the stick spinning after the collision

Answer 1

3.67 rad/s

Step-by-step explanation:

L = Length of meter stick = 1 m

r = Distance at which the bullet will hit the stick =
`(L)/(4)=(1)/(4)`

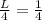
m = Mass of bullet = 3 g

M = Mass of stick = 270 g

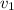`v_1` = Velocity of bullet = 250 m/s

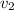`v_2` = Velocity of bullet leaving = 140 m/s

Initial angular momentum

`L_i=mv_1r`

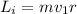
Final angular momentum of the system

`L_f=(1)/(12)ML^2\omega+mv_2r`

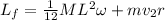
Since, angular momentum is conserved we have

`mv_1r=(1)/(12)ML^2\omega+mv_2r\\\Rightarrow \omega=(12(mv_1r-mv_2r))/(ML^2)\\\Rightarrow \omega=(12(0.003* 250* (1)/(4)-0.003* 140* (1)/(4)))/(0.27* 1^2)\\\Rightarrow \omega=3.67\ rad/s`

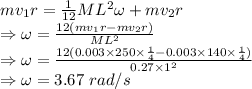
The angular speed is the stick spinning after the collision is 3.67 rad/s