Question

Steam at 100°C is added to ice at 0°C. (a) Find the amount of ice melted and the final temperature when the mass of steam is 14 g and the mass of ice is 45 g.(b) Repeat with steam of mass 1.3 g and ice of mass 45 g.

Answer 1

a) 45g of ice will melt, final temperature of mixture will be 90.8 °C

b) 10.4g of ice will melt, final temperature of mixture will be 0 °C

Step-by-step explanation:

The energy lost by the steam is the sum of the latent heat of vaporization of steam and the energy lost in bringing the temperature of the mixture down to the equilibrium temperature. This is equal to the energy gained by the ice, which is the sum of the latent heat of fusion and the energy gained in raising the temperature of the ice to the equilibrium temperature.

Part a)

`m_(s)=14g` ,
`l_(s,vaporization)=2256J/g` ,
`T_(s,initial)=100\°C`

`m_(i)=45g` ,
`l_(i,fusion)=334J/g` ,
`T_(i,initial)=0\°C`

`C_(w)=4.186 J/g.\°C`

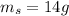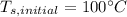
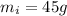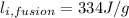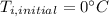
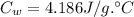
Step 1: Determine energy needed to melt ice

`Q_(1)=m_(i)l_(i,fusion)`

`Q_(1)=45*334`

`Q_(1)=15030 J`

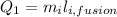
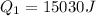
Step 2: Determine energy released during condensation of steam

`Q_(2)=m_(s)l_(s,vaporization)`

`Q_(2)=14*2256`

`Q_(2)=31584 J`

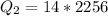
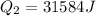
Step 3: Determine temperature of increase of ice water

Energy released in condensation of steam exceeds energy required for melting of ice. Excess energy will raise the temperature of the ice water.

`Q_(2)-Q_(1)=m_(i)c_(w)(T_(iw,final)-T_(i,initial))`

`31584-15030=45*4.184*(T_(iw,final)-0)`

`T_(iw,final)=87.922 \°C`

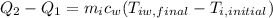
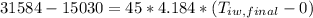
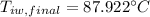
Step 4: Determine average temperature of water

The temperature of water from condensation of steam
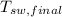`T_(sw,final)` will be 100 °C

`T_(avg)=(m_(i)T_(iw,final)+m_(s)T_(sw,final))/(m_(i)+m_(s))`

`T_(avg)=(45*87.922+14*100)/(45+14)`

`T_(avg)=90.79 \°C`

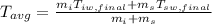
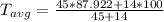
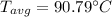
Part b)

`m_(s)=1.3g` ,
`l_(s,vaporization)=2256J/g` ,
`T_(s,initial)=100\°C`

`m_(i)=45g` ,
`l_(i,fusion)=334J/g` ,
`T_(i,initial)=0\°C`

`C_(w)=4.186 J/g.\°C`

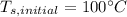
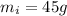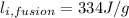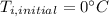
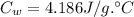
Step 1: Determine energy released during condensation of steam

`Q_(1)=m_(s)l_(s,vaporization)`

`Q_(1)=1.3*2256`

`Q_(1)=2932.7 J`

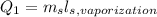
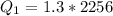
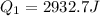
Step 2: Determine energy released during cooling of steam water to 0°C

`Q_(2)=m_(s)c_(w)(T_(sw,initial)-T_(s,final))`

`Q_(2)=1.3*4.184*(100-0)`

`Q_(2)=543.92 J`

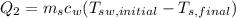
Step 3: Determine mass of ice melted

Energy released by condensation of steam and cooling of water is used to melt ice

`Q_(1)+Q_(2)=m_(i)l_(i,fusion)`

`2932.7+543.92=m_(i)*334`

`m_(i)=10.41 g`

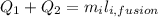
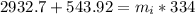
Entire mixture temperature is at 0°C as steam condenses and cools to 0°C, ice melts and remains at 0°C.