Question

The solar system is 25,000 light years from the center of our Milky Way galaxy. One light year is the distance light travels in one year at a speed of 3.0×108m/s. Astronomers have determined that the solar system is orbiting the center of the galaxy at a speed of 230 km/s.

Assuming the orbit is circular, what is the period of the solar system's orbit? Give your answer in years

Answer 1

`T=2.048*10^8` years

Step-by-step explanation:

Period is:

`T=(2*\pi)/(\omega)`

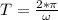
The speed of the galaxy is 230 km/s. Its angular speed is given by:

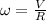`\omega = (V)/(R)` Where R=25000 light years

Now, let N be the amount of seconds in 1 year.

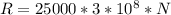`R = 25000 * 3*10^8*N` This value will be in meters.

Replacing this value:

`\omega = (230*10^3)/(75*10^(11)*N)`

`\omega = (3.067*10^(-8))/(N)`

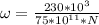
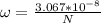
Now, the period will be:

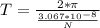`T=(2*\pi)/((3.067*10^(-8))/(N))` This value is in seconds. Since we are asked to give the answer in years, we have to divide by N (amount of seconds in a year:

`T=(2*\pi)/((3.067*10^(-8))/(N))/N`

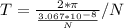
`T=2.048*10^8` years