Question

A test to measure psychotic tendencies was given to a group of 1,000 air force cadets who wished to work in nuclear silos. Any cadet who scored at or over a 64 would be eliminated. The mean of the test was 52 and the standard deviation was 12. Out of the 1000 cadets how many were accepted?

a. 160
b. 340
c. 560
d. 840

Answer 1

Option d) 840

Explanation:

Given that a test to measure psychotic tendencies was given to a group of 1,000 air force cadets who wished to work in nuclear silos.

If Score ≥64 would be eliminated.

X is N(52, 12)

Probability for any random person to get eliminated

=
`P(X\geq 64)\\= 1-R(64)\\=1-0.8413\\= 0.1587`

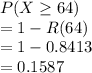
Now coming to sample size of 1000 people, we find each person is independent of the other and there are two outcomes either >64 or < 64

So Y no of persons who get more than 64 is binomial with n =1000 and p = 0.1587

Mean of Y = E(Y)

= no of people who were not accepted
`=1000(0.1587) = 158.7`

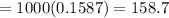
No of people accepted
`= 1000-158.7 = 841.3\\=841`

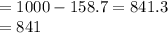
Approximately we get 840 so option d