Answer:
The mid point of segment connecting (-1, -9) and (-10, 4) is

Explanation:
The coordinates of the given points are A(-1,-9) and B (-10,4).
Here, let us assume the point P (x,y) is the mid point of the segment AB.
By MID POINT FORMULA:
The mid point of segments with points ( x1,y1) and (x2,y2) is given as:

So, here the coordinates of P are :
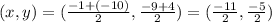
⇒
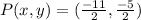
Hence, the mid point of segment connecting (-1, -9) and (-10, 4) is
