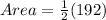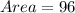Answer:
a) Perimeter
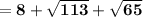
b)Area
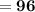
Explanation:
Given ABC is a triangle with vertices at A(-2,-3), B(6,-3) and C(-1,5)
The vertices A(-2,-3), B(6,-3) and C(-1,5) are represented by
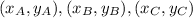 respectively
respectively
Now find the perimeter of the triangle ABC
The perimeter is found by first finding the three distances between the three vertices
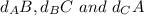 given by
given by
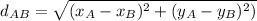
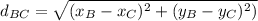
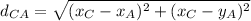
The perimeter is given by
Perimeter
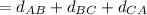
now find
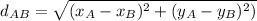
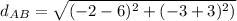
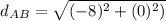
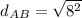
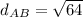
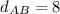
Similarly we find
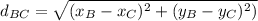
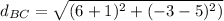
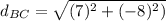
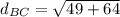
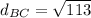
find
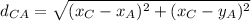
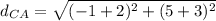
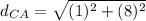
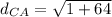
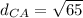
Now adding the distances we get
Perimeter
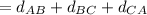
Perimeter
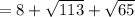
b) Area of the given triangle ABC
The formula for the area of the triangle defined by the three vertices A, B and C is given by:
![Area= (1)/(2) {\det {\left[\begin{array}{ccc}x_A&x_B&x_C\\y_A&y_B&y_C\\1&1&1\end{array}\right]}}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/n5jq53omaki212ev7n83ssaig387jj2se2.png)
where det is the determinant of the three by three matrix.
![Area=(1)/(2){{\det \left[\begin{array}{ccc}-2&6&-1\\ -3& -3&5\\ 1 & 1 & 1\end{array}\right]}}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/y01i7tfk9ee07u94357927yeoo8id8gse3.png)
![Area=(1)/(2)[-2(-3-5)-6(-3-5)-1(-3+3)+3(6+1)-3(-2+1)-5(-2-6)+1(30-3)-1(-10-3)+1(6+18)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/p10tksmqcwi5jv2dbfhmhpj7p1gaqnoanh.png)
![Area=(1)/(2)[-2(-8)-6(-8)-1(0)+3(7)-3(-1)-5(-8)+1(27)-1(-13)+1(24)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/rilhoqq20uvn2ce4dghilgdmtmd0bd8wvr.png)
![Area=(1)/(2)[16+48+0+21+3+40+27+13+24]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7vhtxd5g9hmukyu9a4r13mv8tkgytb6drv.png)