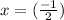Answer:
The solution for the given polynomial
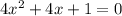 is
is
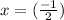
Explanation:
Here, the given quadratic equation is :
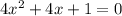
Now, here solving the given equation by SPLITTING THE MIDDLE TERM:
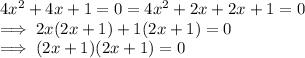
⇒ either (2x+1) = 0, or ( 2x + 1) = 0
⇒ x = -1/2 or x = -1/2
Here, in both the cases, the value of x is equal i.e x = -1/2
So, the given function has TWO IDENTICAL ROOTS.
Hence the solution for the given polynomial
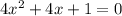 is
is