Question

line segment with one endpoint at (2,5) is divided in the ratio 4:5 by the point (10,1). which coordinates could represent the other endpoint.

Answer 1

20, 4

Explanation:

Answer 2

(20,-4)

Explanation:

We are given;

One end point as (2,5)

Point of division as (10,1)

The ratio of division as 4:5

We are required to calculate the other endpoint.

Assuming the other endpoint is (x,y)

Using the ratio theorem

If the unknown endpoint is the last point on the line segment;

Then;

`\left[\begin{array}{ccc}10\\1\end{array}\right]`=
`(4)/(5) \left[\begin{array}{ccc}x\\y\end{array}\right]`+
`(5)/(9)\left[\begin{array}{ccc}2\\5\end{array}\right]`

Therefore; solving the equation;

`10=(4)/(9)x+(10)/(9)`

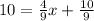
solving for x

x = 20

Also

`1=(4)/(9)y+(25)/(9)`

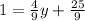
solving for y

y= -4

Therefore,

the coordinates of the end point are (20,-4)