Question

A shipping service restricts the dimensions of the boxes it will ship for a certain type of service.

The restriction states that for boxes shaped like rectangular prisms, the sum of the perimeter of the base of the box and the height of the box cannot exceed 130 inches. The perimeter of the base is determined using the width and length of the box. If a box has a height of 60 inches and its length is 2.5 times the width, which inequality shows the allowable width x, in inches, of the box?
(STEP-BY-STEP)
ANSWER CHOICES

A. 0 B. 0 C. 0 D. 0

Answer 1

Then the answer is option a

a. 0<x
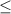`\leq`10

Explanation:

perimeter + height is less than 130 inches.

If height is 60 inches.then perimeter left is 70 inches.

If perimeter was more than 70 inches then perimeter 60 more than the height would be more than 130.

perimeter of rectangle is

It has two widths and two lengths because that's what rectangles do.

width of base "x"

Then the length is 2.5x

perimeter = 2 width + 2 length

=
`2(x) + 2(2.5x)`

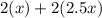
= 2x + 5x

= 7x

but perimeter can't be more than 70 inches.

So x can't be more than 10 inches because if x was more than 10 inches, then 7x which is perimeter would be more than 70 inches.

`2x + 2(2.5x) + 60 \leq 130`

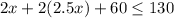
7x + 60 ≤ 130

7x ≤ 70

x ≤ 10

Then the answer is option a

a. 0<x≤10