Question

the passengers in a roller coaster feel 50 heavier than their true weight as the car goes through a dip with a 30m radius of curvature. What is the car's speed at the bottom of the dip?

Answer 1

v = 12.12 m/s

Step-by-step explanation:

Given that,

Radius of the curvature, r = 30 m

To find,

The car's speed at the bottom of the dip.

Solution,

Let mg is the true weight of the passenger. When it is moving in the circular path, the centripetal force act on it. It is given by :

`F=(mv^2)/(r)`

The normal reaction of the passenger is given by :

`N=mg-50\%mg`

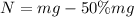
N = 1.5 mg

Let v is the car's speed at the bottom of the dip. It can be calculated as:

`1.5\ mg-mg=(mv^2)/(r)`

`v=√(0.5gr)`

`v=√(0.5* 9.8* 30)`

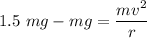
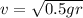
v = 12.12 m/s

So, the speed of the car at the bottom of the dip is 12.12 m/s. Hence, this is the required solution.