Question

For every positive even integer n, the function h(n) is defined to be the product of all the even integers from 2 to n, inclusive. If p is the smallest prime factor of h(100) + 1, then p is ____.

Answer 1

More than 50

Explanation:

To solve, we need to first see that the function is h(n). Picking main points from the question statement:

• h(n) is the product of all even integers (From 2 to n)

• p is the smallest factor of h(100)+1
• h(100)+1 , here n=100

From here, we can write h(100) as:

h(100) =
`2 * 4 * 6 * 8 * ...... * 100`

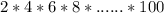
h(100) =
`2^(50) * (1*2*3*......*50)`=
`2^(50) * 50!`

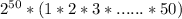so,

h(100)+1 =
`(2^(50) * 50! )+1`

Now two numbers,

h(100) and h(100)+1 are consecutive integers and since they are consecutive so they are co-prime. Hence they only have common factor of 1. Example, 13 and 14 have only common factor of 1

As h(100) has all prime numbers from 1 to 50 and according to above statement h(100)+1 won't have any prime factor from 1 to 50, so the smallest prime factor p is greater than 50.