Question

A shark is swimming 28 feet below sea level. If the angle of

depression from a boat on the water to the shark is 13º, what is the
horizontal distance between the boat and the shark?

Answer 1

121.28 feet

Explanation:

See the diagram attached.

Let B is the position of the boat and BA = 28 feet is the height of the water surface from the level of the shark.

If the position of the shark is at S then angle of depression from boat to the sherk i.e. ∠ OBS = 13° and we have ∠ BSA = ∠ OBS = 13° {Alternate angles}

Now, using trigonometry in right triangle Δ ABS we can write,

`\tan 13 = (AB)/(AS) = (28)/(AS)`

⇒
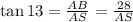
`AS = (28)/(\tan 13) = 121.28` feet.

Therefore, the horizontal distance between the boat and the shark is AS = 121.28 feet, (Answer)

Answer 2

The horizontal distance between boat and the shark is 121.28 feet

Explanation:

Given as :

The Distance of the shark swimming below sea level = AB = 28 feet

The angle of depression from a boat on water to shark = 13°

Let The horizontal distance between shark and boat = OA = x

Now, Tan angle =
`(\textrm Perpendicular)/(\textrm base)`

or, Tan 13° =
`(\textrm OA)/(\textrm AB)`

Or, Tan 13° =
`(\textrm 28)/(\textrm x)`

Or, 0.2308 =
`(\textrm 28)/(\textrm x)`

Or, x =
`(28)/(0.2308)`

∴ x = 121.28 feet

So The horizontal distance = x = 121.28 feet

Hence The horizontal distance between boat and the shark is 121.28 feet Answer