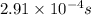Answer with Explanation:
We are given that
Inner radius of wooden toroidal core=
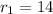 cm
cm
Outer radius of wooden toroidal core=
 cm
cm
Diameter of wire=1.0 mm
Resistance per meter=0.020 ohm/m
a.We have to find the inductance of the toroid.
Inner circumference of toroid=
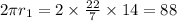 cm=880 mm
cm=880 mm
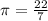
1 cm=10 mm
Number of turns is roughly ,N=
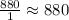
h=
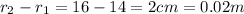
1 m=100 cm
Inductance of the toroid=

Substitute the values then, we get
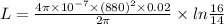
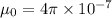
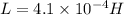
Hence, the inductance of the toroid=
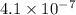 H
H
b.We have to find the inductive time constant of toroid.
Total length of wire=
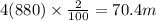
Because, total number of turns=880
Perimeter of square = 4 times the side of the square
Side of square shaped loop=2 cm
Resistance of wire=
 ohm
ohm
Inductive time constant
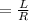
Inductive time constant=
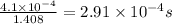
Hence, the inductive time constant of toroid=